§27 General description of the problem

Consider two plane parallel infinite tangential discontinuities. The cloud, or internal region to the tangential discontinuities has uniform pressure $p_c$ and density $\rho_c$. The environment, or external region to the cloud has also uniform values of pressure $p_1$ and density $\rho_1$ respectively. A plane parallel shock wave is travelling in the positive $x$ direction and eventually will collide with the left boundary of the cloud at time $t \! = \! t_0 \! < \! 0$. By definition, the density of the cloud is greater than that of the environment. Knowing the pressure $p_2$ and density $\rho_2$ behind the shock wave, it is possible to solve the hydrodynamical problem thus defined.

The problem of the collision of a shock wave and a tangential discontinuity is well known (Landau & Lifshitz, 1995) and was first discussed by Hugoniot in 1885. Since at the instantaneous time of collision the values of, say, the density in front and behind the shock are $\rho_c$ and $\rho_2$ respectively, the standard jump conditions for a shock no longer hold. A discontinuity in the initial conditions (first initial discontinuity) occurs.

When a discontinuity in the initial conditions occurs, the values of the hydrodynamical quantities need not to have any relation at all between them at the surface of discontinuity. However, certain relations need to be valid in the gas if stable surfaces of discontinuity are to be created. For instance, the Rankine-Hugoniot relations have to be valid in a shock wave. What happens is that this initial discontinuity splits into several discontinuities, which can be of one of the three possible types: shock wave, tangential discontinuity or weak discontinuity. These newly formed discontinuities move apart from each other with respect to the plane of formation of the initial discontinuity.

Very general arguments show that only one shock wave or a pair of weak discontinuities bounding a rarefaction wave can move in opposite directions with respect to the point in which the initial discontinuity took place. For, if two shock waves move in the same direction, the shock at the front would have to move, relative to the gas behind it, with a velocity less than that of sound. However, the shock behind must move with a velocity greater than that of sound with respect to the same gas. In other words, the leading shock will be overtaken by the one behind. For exactly the same reason a shock and a rarefaction wave cannot move in the same direction, due to the fact that weak discontinuities move at the velocity of sound relative to the gas they move through. Finally, two rarefaction waves moving in the same direction cannot become separated, since the velocities of their boundaries with respect to the gas they move through is the same.

Boundary conditions demand that a tangential discontinuity must remain at the point where the initial discontinuity took place. This follows from the fact that the discontinuities formed as a result of the initial discontinuity must be such that they are able to take the gas from a given state at one side of the initial discontinuity to another state in the opposite side. The state of the gas in any one dimensional problem in hydrodynamics is given by three parameters (say the pressure, the density and the velocity of the gas). A shock wave however, is represented by only one parameter as can be seen from the shock adiabatic relation (Hugoniot adiabatic) for a polytropic gas (c.f. eq.(13.19)):

$${\frac{\ensuremath{\mathit{V}}_b}{\ensuremath{\mathit{V}}_f}} = { \frac{(\kappa+1)p_f + (\kappa-1)p_b} {(\kappa-1)p_f + (\kappa+1)p_b} },$$ (27.1)

where $p$ and $\ensuremath{\mathit{V}}$ stand for pressure and specific volumes respectively, $\kappa$ is the polytropic index of the gas and the subscripts $f$ and $b$ label the flow in front of and behind the shock. For a given thermodynamic state of the gas (i.e. for given $p_f$ and $\ensuremath{\mathit{V}}_f$) the shock wave is determined completely since, for instance, $p_b$ would depend only on $\ensuremath{\mathit{V}}_b$ according to the shock adiabatic relation. On the other hand, a rarefaction wave is also described by a single parameter. This is seen from the equations which describe the gas inside a rarefaction wave which moves to the left with respect to gas at rest beyond its right boundary (c.f. eqs.(14.11)-(14.14)):

$$c_R = c_4 + {\frac{1}{2}} (\kappa_c-1) w_R,$$ (27.2)

$$\rho_R = \rho_4 \left\{ 1 + { \frac{1}{2}} \frac{(\kappa_c -1) w_R}{ c_4} \right\} ^ { 2 / (\kappa_c -1) },$$ (27.3)

$$p_R = p_4 \left\{ 1 + { \frac{1}{2}} \frac{(\kappa_c -1) w_R}{ c_4} \right\} ^ { 2\kappa_c / (\kappa_c -1)},$$ (27.4)

$$w_R = { -{ \frac{2}{\kappa_c +1} } \left(c_4 + {\frac{x}{t}} \right) }.$$ (27.5)

where $c_4$ and $c_R$ represent the sound speed behind and inside the rarefaction wave respectively. The magnitude of the velocity of the flow inside the rarefaction wave is $w_R$ in that system of reference. The quantities $p_4$ and $p_R$ are the pressures behind and inside the rarefaction wave respectively. The corresponding values of the density in the regions just mentioned are $\rho_4$ and $\rho_R$.

With two undetermined parameters, it is not possible to give a description of the thermodynamic state of the gas. It is the tangential discontinuity, which remains where the initial discontinuity was produced, that accounts for the third parameter needed to describe the state of the fluid.

When a shock wave hits a tangential discontinuity, a rarefaction wave cannot be transmitted to the other side of the gas bounded by the tangential discontinuity. For, if there were a transmitted rarefaction wave to the other side of the tangential discontinuity, the only possible way the boundary conditions could be satisfied is if a rarefaction wave is reflected back to the gas. In other words, two rarefaction waves separate from each other in opposite directions with respect to the tangential discontinuity that is left after the interaction. In order to show that this is not possible, consider a shock wave travelling in the positive $x$ direction, which compresses gas $1$ into gas $2$ and collides with a tangential discontinuity. After the interaction two rarefaction waves separate from each other and a tangential discontinuity remains between them. In the system of reference where the tangential discontinuity is at rest, the velocity of gas $2$ is given by $\ensuremath{v}_2 = \! - \int_{p_3}^{p_2} \sqrt{ -{\rm d}p{\rm d}\ensuremath{\mathit{V}}}$, according to eq.(14.5), where $p_3$ is the pressure of gas $3$ surrounding the tangential discontinuity. Accordingly, the velocity of gas $1$ in the same system of reference is $\ensuremath{v}_1 \! = \! - \int_{p_3}^{p_1} \sqrt{ -{\rm d}p{\rm d}\ensuremath{\mathit{V}}}$. Since the product $-{\rm d}p{\rm d}\ensuremath{\mathit{V}}$ is a monotonically increasing function of the pressure and $0 \le p_3 \le p_1$ then:

$$-\int_0^{p_2} \sqrt{ - {\rm d}P {\rm d}\ensuremath{\mathit{V}}} \... ...t{V}}} - \int_{p_1}^{p_2} \sqrt{ - {\rm d}P {\rm d}\ensuremath{\mathit{V}}}.$$

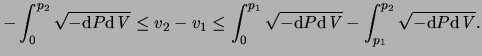
The difference in velocities $\ensuremath{v}_1 - \ensuremath{v}_2$ has the same value in any system of reference and so, it follows that $\ensuremath{v}_1 \! \le \! \ensuremath{v}_2$, in particular in a system of reference in which the incident shock is at rest. However, for the incident shock to exist, it is necessary that $\ensuremath{v}_1 \! > \! \ensuremath{v}_2$, and so two rarefaction waves cannot be formed as a result of the interaction.

So far, it has been shown that after the collision between the shock and the boundary of the cloud, a first initial discontinuity is formed. This situation cannot occur in nature and the shock splits into a shock which penetrates the cloud and either one of a shock, or a rarefaction wave (bounded by two weak discontinuities) is reflected from the point of collision. With respect to the point of formation of the initial discontinuity, the boundary conditions demand that a tangential discontinuity must reside in the region separating the discontinuities previously formed.

In a shock wave, the velocities ( $\ensuremath{v}$) in front and behind the shock are related to one another by their difference:

$${\ensuremath{v}_f-\ensuremath{v}_b}=\sqrt{(p_b-p_f)(\ensuremath{\mathit{V}}_f-\ensuremath{\mathit{V}}_b)},$$ (27.6)

according to eq.(13.20) where the subscripts $f$ and $b$ label the flow of the gas in front and behind the shock wave.

If after the first initial discontinuity two shock waves separate with respect to the point of collision, then according to eq.(27.6) the velocities of their shock front flows are given by $\ensuremath{v}_c \! = \! -\sqrt{ ( p_3 - p_1 ) ( \ensuremath{\mathit{V}}_c - \ensuremath{\mathit{V}}_{3'} ) }$ and $\ensuremath{v}_2 \! = \! \sqrt{ ( p_3 - p_2 ) ( \ensuremath{\mathit{V}}_2 - \ensuremath{\mathit{V}}_3 ) }$, where the regions $3$ and $3'$ bound the tangential discontinuity which is at rest in this particular system of reference (see top and middle panels of fig.(V.1)). Due to the fact that $p_3 \ge p_2$ and because the difference $\ensuremath{v}_2 - \ensuremath{v}_c$ is a monotonically increasing function of the pressure $p_3$, then:

$$\ensuremath{v}_2 - \ensuremath{v}_c > ( p_2 -p_1 ) \surd \left\{2... ... \kappa_c - 1 \right) p_1 + \left( \kappa_c + 1 \right) p_2 \right] \right\},$$

according to the shock adiabatic relation. Since $\ensuremath{v}_2 \! - \ensuremath{v}_c$ is given by eq.(27.6), then:

$${ \frac{\ensuremath{\mathit{V}}_1}{(\kappa-1)+(\kappa+1)p_2/p_1}} > { \frac{\ensuremath{\mathit{V}}_c}{(\kappa_c-1)+(\kappa_c+1)p_2/p_1} },$$ (27.7)

where $\kappa$ and $\kappa_c$ represent the polytropic indexes of the environment and the cloud respectively. $\ensuremath{\mathit{V}}_1$ and $\ensuremath{\mathit{V}}_c$ are the specific volumes on the corresponding regions. In other words, a necessary and sufficient condition to have a reflected shock from the boundary of the two media, under the assumption of initial pressure equilibrium between the cloud and the environment, is given by eq.(27.7). Since for the problem in question $\ensuremath{\mathit{V}}_1\!>\!\ensuremath{\mathit{V}}_c$ and the polytropic indexes are of the same order of magnitude, a reflected shock is produced.

In the same way, at time $t\!=\!0$ when the transmitted shock reaches the right tangential discontinuity located at $x \! = \! 0$, another (second) initial discontinuity must occur. In this case, we must invert the inequality in eq.(27.7), change $\kappa$ by $\kappa_c$ and $p_2$ by $p_3$, where $p_3$ is the pressure behind the shocks produced by the first initial discontinuity. Again, using the same argument for the polytropic indexes, it follows that after this interaction a rarefaction wave bounded by two weak discontinuities must be reflected from the boundary between the two media. As a result of the interaction, once again, the boundary conditions demand that a tangential discontinuity remains between the newly formed discontinuities.

This situation continues until the rarefaction wave and the left tangential discontinuity of the cloud collide at time $t\!=\!\tau\!>\!0$. At this point, two rarefaction waves separating from each other from the point of formation will be produced once a stationary situation is reached, and a tangential discontinuity will separate the newly formed discontinuities. One could continue with the solution for further reflections of the shock and rarefaction waves but, for the sake of simplicity, the calculations are stopped at this point. Fig.(V.1) shows a schematic description of the solution described above in a system of reference such that the tangential discontinuities which are left as a result of the different interactions are at rest. The numbers in the figure label different regions in the flow. A more detailed analysis follows in sections §28 and §29.

Figure V.1: An incoming shock travelling to the right (top panel) hits a tangential discontinuity at time $t_0\!<\!0$. This produces two shocks moving in opposite directions with respect to the place of formation (middle panel). When the transmitted shock into the cloud (region C) collides with its right boundary a reflected rarefaction wave (region R) bounded by two tangential discontinuities and a shock transmitted to the external medium (lower panel) are formed. Arrows represent direction of different boundaries, or the flow itself. The numbers in the figure label different regions of the flow. Dashed lines represent shocks, dash-dot are weak discontinuities and continuous ones are tangential discontinuities. The system of reference is chosen such that the tangential discontinuities which are left as a result of the collisions are always at rest.