§29 Second initial discontinuity

Let us now analyse the situation for which $0 \! < \! t\! < \! \tau$. To begin with let us prove that:

$$w_1 < \ensuremath{v}_2 + \ensuremath{v}_c \equiv u_2 ,$$ (29.1)

where the velocities $w_1$, $\ensuremath{v}_2$ and $\ensuremath{v}_c$ are defined in fig.(V.1). Suppose that the inequality in eq.(29.1) is not valid, then, by expressing the velocities as function of the specific volumes and pressures by means of eq.(27.6) and the fact that $p_2 \! > \! p_1$, $p_3 \! > p_4$ and $\ensuremath{\mathit{V}}_{4'} \! > \! \ensuremath{\mathit{V}}_3$, it follows that $\rho_3 > \! \rho_c$; then as the cloud's density grows without limit, so does $\rho_3$. Necessarily, eq.(29.1) has to be valid for sufficiently small values of the cloud's specific volume. It is important to point out that since $w_2 \! = \! \vert u_2 \! - \! w_1 \vert \! = \! u_2 \! - \! w_1$, the gas in region 2 as drawn in fig.(V.1) travels in the positive $x$ direction. According to fig.(V.1), flows in region $1$ and $3$ are related by

$$w_1 - w_3 = \ensuremath{v}_c,$$ (29.2)

Let us now prove a very general property of the solution. Regions $2$ and $3$ are related to one another by the shock adiabatic relation. Since the gas in regions $3'$ and $4$ obey a polytropic equation of state $p_3 / p_4 \! = \! \left( \ensuremath{\mathit{V}}_4 / \ensuremath{\mathit{V}}_{3'} \right)^{\kappa_c}$, it follows that:

$$\frac{p_4}{p_2} = { { \left( \frac{ \ensuremath{\mathit{V}}_{3'} ... ...kappa+1)\ensuremath{\mathit{V}}_3 - (\kappa-1)\ensuremath{\mathit{V}}_2 } } }.$$

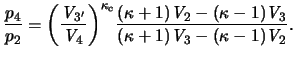
Now, due to the fact that $\ensuremath{\mathit{V}}_{3'} \! < \! \ensuremath{\mathit{V}}_4 \! < \! \ensuremath{\mathit{V}}_1$, $\ensuremath{\mathit{V}}_3 \! < \! \ensuremath{\mathit{V}}_2 \! < \! \ensuremath{\mathit{V}}_1$ and $\kappa, \kappa_c \! > \! 1$ for a reasonable equation of state, this relation can be written

$$\frac{p_4}{p_2} < { \frac{1}{2} \left[-(\kappa-1)+(\kappa+1) \fra... ...emath{\mathit{V}}_1} \right] \to 0 , {\rm as} \; \frac{p_1}{p_2} \to 0 }$$ (29.3)

with the aid of the shock adiabatic relation. This result implies that most of the energy of the incoming shock has been injected to the cloud, no matter how strong the initial incident shock is. Only a very small fraction of this energy is transmitted to the external gas that lies in the other side of the cloud. Note that this result is of a very general nature since no assumptions about the initial density contrast of the environment were made. This is an important conclusion. All the energy of the shock is dissipated inside the cloud and so it is important for cloud heating.

In order to continue with a solution at first order approximation in $\ensuremath{\mathit{V}}_c$, note that we have to use eqs.(28.6)-(28.8) together with:

$$p_4 = p_1 + p_4^\star ,$$ (29.4)

$$\ensuremath{\mathit{V}}_4 = \ensuremath{\mathit{V}}_4^\star ,$$ (29.5)

$$\ensuremath{\mathit{V}}_{4'} = \ensuremath{\mathit{V}}_1 + \ensuremath{\mathit{V}}_{4'}^\star,$$ (29.6)

where the quantities with a star are of first order. The velocities $w_1$ and $w_3$ can be expressed as functions of the specific volumes and pressures by means of eq.(27.6), from which after substitution of eqs.(29.4)-(29.6) it follows that:

$$w_1^2 = -p_4^\star \ensuremath{\mathit{V}}_{4'}^\star ,$$ (29.7)

$$w_3 = { { \frac{2}{\kappa_c - 1} } \left( \sqrt{\kappa_c p_{3_0} ... ...}_{3'}^\star } - \sqrt{\kappa_c p_1 \ensuremath{\mathit{V}}_4^\star} \right) }.$$ (29.8)

The specific volumes behind the transmitted shock and the reflected rarefaction wave are obtained from the shock adiabatic relation and the polytropic equation of state for the gas inside the rarefaction wave:

$$\ensuremath{\mathit{V}}_{4'}^\star = -\ensuremath{\mathit{V}}_1 \frac{ p_4^\star }{ \kappa p_1 } ,$$ (29.9)

$$\ensuremath{\mathit{V}}_4^\star = \ensuremath{\mathit{V}}_{3'}^\star \left( \frac{ p_{3_0} }{ p_{1} } \right)^{1/\kappa_c}.$$ (29.10)

By substitution of eqs.(29.7)-(29.10) and eq.(28.4) in eq.(29.2) the required solution is found:

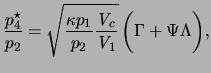$$\frac{p_4^\star}{p_2} = { \sqrt{ \frac{\kappa p_1}{p_2} \frac{\en... ...t{V}}_c}{\ensuremath{\mathit{V}}_1} } \bigg( \Gamma + \Psi \Lambda \bigg), }$$ (29.11)
where:

$$\Psi=\frac{ 2 \sqrt{\kappa_c} }{\kappa_c - 1} { \sqrt{ \frac { (\... ... 1)p_{3_0}/p_2 } { (\kappa_c - 1)p_1/p_2 + (\kappa_c + 1)p_{3_0}/p_2 } } } ,$$

$$\Gamma=\frac{ \sqrt{2} (p_{3_0} - p_1)/p_2 }{ \sqrt { (\kappa_c-1)p_1/p_2 + (\kappa_c+1)p_{3_0}/p_2 } } ,$$

$$\Lambda=\sqrt{ \frac{ p_{3_0} }{p_2} } - \sqrt{ \frac{p_1}{p_2} \left( \frac{p_{3_0}}{p_{1}} \right)^{1/\kappa_c} } .$$

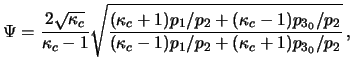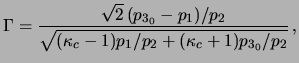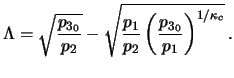For completeness, the limits for the case of strong and weak incident shocks are given:

$$\frac{ p_4^\star }{ p_2 } = \sqrt{ \frac{ \kappa ( 3 \kappa - 1 )... ...th{\mathit{V}}_c }{ \ensuremath{\mathit{V}}_1 } } \bigg( \sqrt{2} + \xi \bigg),$$ (29.12)

$$\frac{p_4^\star}{p_2} = { 6 \zeta \sqrt{ \frac{\kappa}{ \kappa_c } }\sqrt{ \frac{\ensuremath{\mathit{V}}_c}{\ensuremath{\mathit{V}}_1} } },$$ (29.13)
with:

$$\xi=\frac{ 2 \sqrt{\kappa_c} }{ \sqrt{ (\kappa_c - 1) } } \left[ ... ... \frac{\kappa-1}{3\kappa-1} \right)^ { (\kappa_c-1) / { 2 \kappa_c } } \right].$$

It follows from eq.(29.12) that $p_4 \! \ll \! p_2$ as the strength of the incident shock increases without limit. This result was given by the very general argument of eq.(29.3). Fig.(V.3) shows the variation of the pressure $p_4$ behind the shock transmitted to the environment as a function of the strength of the initial incident shock, after the second initial discontinuity.

Figure V.3: Variation of the pressure $p_4$ behind the transmitted shock into the external medium as a function of the strength of the incident shock. The continuous line represents the case for which the cloud has infinite density and so it does not transmit any shock to the external medium. The dashed curve represents the case for which the cloud's specific volume is a quantity of the first order. The dash-dotted curve is the limit for which a strong (or weak) incident shock collides with the cloud at the same order of approximation. The perturbed curves were produced under the assumption that $\rho_c/\rho_1\!=\!100$ for monoatomic gases.