§28 First initial discontinuity

According to fig.(V.1), after the first initial discontinuity the absolute values of the velocities ( $\ensuremath{v}$) of the flow are related by:

$$\ensuremath{v}_2 + \ensuremath{v}_c = \ensuremath{v}_{2i}.$$ (28.1)

With the aid of eq.(27.6), the velocities of eq(28.1) are given by:

$$\lefteqn{ \ensuremath{v}_{2i}^2 = (p_2-p_1)(\ensuremath{\mathit{V}}_1-\ensuremath{\mathit{V}}_2), }$$ (28.2)

$$\lefteqn{ \ensuremath{v}_c^2 = (p_3-p_1)(\ensuremath{\mathit{V}}_c-\ensuremath{\mathit{V}}_{3'}), }$$ (28.3)

$$\lefteqn{ \ensuremath{v}_2^2 = (p_3-p_2)(\ensuremath{\mathit{V}}_2-\ensuremath{\mathit{V}}_{3}). }$$ (28.4)

Inserting eqs.(28.2)-(28.4) into eq.(28.1) and substituting for the specific volumes from eq.(27.1), one ends up with a relation which relates the pressure $p_3$ as a function of $p_2$, $p_1$ and the polytropic indexes in an algebraic linear form. Straightforward manipulations show that the resulting equation does not have an easy analytic solution, even for the particular cases in which a strong or weak incident shock collides with the cloud.

In order to find a set of analytic solutions, let us first describe a particular solution to the problem. If we consider a cloud with an initial infinite density -a solid wall, then eq.(28.1) takes the form $\ensuremath{v}_2 \! =\! \ensuremath{v}_{2i}$, and a ``zeroth order'' solution is found (Landau & Lifshitz, 1995):

$$\frac{ p_{3_0} }{p_2} = { \frac{ (3\kappa-1)p_2 - (\kappa-1)p_1 }{ (\kappa-1)p_2 + (\kappa+1)p_1 } },$$ (28.5)

where $p_{3_0}$ is the value of the pressure behind the reflected and transmitted shocks for the case in which the cloud has specific volume $\ensuremath{\mathit{V}}_c \! = \! 0$. For this particular case, eq.(28.5) determines $p_{3_0}$ as a function of $p_1$ and $p_2$, which are initial conditions to the problem. Due to the fact that the gas is polytropic, this relation is the required solution to the problem.

In order to find a solution more appropriate to the general case, we can make the approximation that $\ensuremath{\mathit{V}}_c$ is a first order quantity, that is:

$$p_3 = p_{3_0} + p_3^\star,$$ (28.6)

$$\ensuremath{\mathit{V}}_3 = \ensuremath{\mathit{V}}_{3_0} + \ensuremath{\mathit{V}}_3^\star,$$ (28.7)

$$\ensuremath{\mathit{V}}_{3'} = \ensuremath{\mathit{V}}_{3'}^\star,$$ (28.8)

where the quantities with a star are of the first order and the subscript 0 represents the values at zeroth order approximation. Substituting eqs.(28.6)-(28.8) into eqs.(28.3)-(28.4) gives:

$$\ensuremath{v}_2^2 = \ensuremath{v}_{2o}^2 - \ensuremath{\mathit{... ... p_2) + p_3^\star ( \ensuremath{\mathit{V}}_2 -\ensuremath{\mathit{V}}_{3_0} ),$$ (28.9)

$$\ensuremath{v}_c^2 = (p_{3_0} - p_1)(\ensuremath{\mathit{V}}_c-\ensuremath{\mathit{V}}_{3'}^\star).$$ (28.10)

From the shock adiabatic relation, eq.(27.1), and eqs.(28.6)-(28.8) it follows that

$${ \frac{ \ensuremath{\mathit{V}}_{3_0} }{\ensuremath{\mathit{V}}_... ...kappa + 1)p_2 + (\kappa-1)p_{3_0} }{ (\kappa - 1)p_2 + (\kappa + 1)p_{3_0} } },$$ (28.11)

$${ \frac{ \ensuremath{\mathit{V}}_{3'}^\star }{\ensuremath{\mathit... ... + 1)p_1 + (\kappa_c - 1)p_{3_0} } { (\kappa_c-1)p_1 + (\kappa_c+1)p_{3_0} } },$$ (28.12)

$${ \frac{ \ensuremath{\mathit{V}}_3^\star}{\ensuremath{\mathit{V}}... ...4\kappa p_2 p_3^\star}{ \left[ (\kappa-1)p_2 + (\kappa+1)p_{3_0} \right]^2 } }.$$ (28.13)

Substituting eqs.(28.9)-(28.10) and eq.(28.13) in eq.(28.1) gives the required solution:

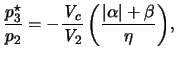$${ \frac{p_3^\star}{p_2} }= -{ \frac{\ensuremath{\mathit{V}}_c}{\e... ...math{\mathit{V}}_2} \left( \frac{ \vert{\alpha}\vert + \beta }{\eta} \right) },$$ (28.14)
where:

$$\beta = \left( {\frac{ p_{3_0} }{p_2} } - { \frac{p_1}{p_2} } \ri... ...\frac{ \ensuremath{\mathit{V}}_{3'}^\star }{\ensuremath{\mathit{V}}_c} \right),$$

$$\eta = { \left(1-{ \frac{ \ensuremath{\mathit{V}}_{3_0} }{\ensure... ...{3_0}/\ensuremath{\mathit{V}}_2 }{ (\kappa -1) + (\kappa + 1)p_{3_0}/p_2 } } },$$

$$\vert{\alpha}\vert^2 = 4 \frac{\ensuremath{\mathit{V}}_2}{\ensure... ...\frac{ \ensuremath{\mathit{V}}_{3'}^\star }{\ensuremath{\mathit{V}}_c} \right).$$

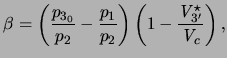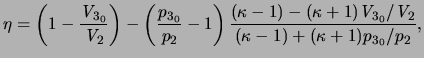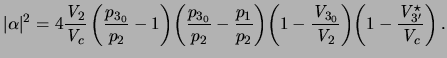The specific volumes $\ensuremath{\mathit{V}}_{3_0}$ and $\ensuremath{\mathit{V}}_{3'}^\star$ are given by eq.(28.11) and eq.(28.12) respectively. For completeness, approximations to eq.(28.14) for the case of a very strong incident shock and that of a weak incident shock are given:

$$\frac{p_3^\star}{p_2} = - { { \frac{ 4\kappa^2 (\kappa+1) } { (3\... ...hit{V}}_1} } \left( \frac{3\kappa -1}{\kappa_c+1} + \mathit{k} \right), }$$ (28.15)

$$\frac{ p_3^\star}{p_1} = - { 2 \zeta \frac{\kappa}{\kappa_c} \sqr... ...sqrt { \frac{\ensuremath{\mathit{V}}_c}{\ensuremath{\mathit{V}}_1} } \right), }$$ (28.16)
where:

$$\mathit{k} = 2 \sqrt{ \frac{\ensuremath{\mathit{V}}_1}{\ensurem... ...it{V}}_c} { \frac{ (3\kappa-1) (\kappa-1) }{ (\kappa_c+1) (\kappa+1) } } } ,$$

and $\zeta \! \equiv \! (p_2 \! - \! p_1)/p_1 \! \ll 1$ in the weak limit. Fig.(V.2) shows a plot of the pressure $p_3$ as a function of the strength of the incident shock. It is interesting to note that even for very strong incident shocks the ratio $p_3/p_2$ differs from zero, which follows directly from eq.(28.5) and eq.(28.15). This simply means that the reflected shock is not strong, no matter what initial conditions were chosen.

Figure V.2: Variation of the pressure $p_3$ behind the transmitted shock into the cloud as a function of the strength of the initial incident shock. The continuous line shows the case for which the cloud is a solid wall with infinite density. The dashed curve is the solution at first order approximation in which the cloud's specific volume is a first order quantity. The acoustic approximation in which the incident shock is weak, to the same order of accuracy, is represented by a dot-dashed curve. The perturbed solutions were plotted assuming $\rho_c/\rho_1\!=\!100$ for polytropic indexes $\kappa \! = \! \kappa_c \! = 5/3$, corresponding to a monoatomic gas.

There are certain important general relations which follow from these results. Firstly, by definition the pressure $p_2$ behind the shock is greater than the pressure $p_1$ of the environment. Now consider a strong incident shock. Since $p_3 \! > \! p_2 \! \gg \! p_1$, it follows that the shock transmitted into the cloud is very strong. Also, the reflected shock does not have to compress the gas behind it too much to acquire the required equilibrium and so, it is not a strong shock. This last statement is in agreement with eq.(28.15). In general, for any strength of the incident shock, since the inequality $p_3 \! > p_2 \! > \! p_1$ holds, continuity demands that the reflected shock cannot be strong and, more importantly, that the penetrating shock is always stronger than the reflected one.

Secondly, very general inequalities are satisfied by the velocities $\ensuremath{v}_2$, $\ensuremath{v}_c$, $\ensuremath{v}_{sl}$ as defined in fig.(V.1). For instance:

$$\ensuremath{v}_{sl} \! > \! \ensuremath{v}_2.$$ (28.17)

This result follows from the fact that $\ensuremath{\mathit{V}}_3 \ensuremath{v}_2 / (\ensuremath{\mathit{V}}_3 - \! \ensuremath{\mathit{V}}_2) \! > \! \ensuremath{v}_2$ holds, and the left hand side of this inequality is just $\ensuremath{v}_{sl}$ according to mass flux conservation across the reflected shock.

On the other hand, from eq.(28.3) and eq.(28.4), since $p_2 \! > \! p_1$ it follows that a necessary and sufficient condition for $\ensuremath{v}_2 \! > \! \ensuremath{v}_c$ to be true is that $\ensuremath{\mathit{V}}_2 \! - \! \ensuremath{\mathit{V}}_3 \! > \! \ensuremath{\mathit{V}}_c \! - \! \ensuremath{\mathit{V}}_{3'}$. This last condition is satisfied for sufficiently small values of $\ensuremath{\mathit{V}}_c$. To give an estimate of the smallness of the cloud's specific volume needed, note that a necessary and sufficient condition for $\ensuremath{\mathit{V}}_2 \! - \! \ensuremath{\mathit{V}}_3 \! > \! \ensuremath{\mathit{V}}_c \! - \! \ensuremath{\mathit{V}}_{3'}$ to be valid is:

$${ \frac{ \ensuremath{\mathit{V}}_2 (p_3 - p_2) }{ (\kappa-1)p_2 +... ...{ \ensuremath{\mathit{V}}_c (p_3-p_1) }{ (\kappa_c-1)p_1 + (\kappa_c+1)p_3 } },$$ (28.18)

according to the shock adiabatic relation for the transmitted and reflected shocks. Since $p_3 \! > \! p_2 \! > \! p_1$ and $\ensuremath{\mathit{V}}_2 \! < \! \ensuremath{\mathit{V}}_1$ it follows that:

$$\frac{\ensuremath{\mathit{V}}_1}{ (\kappa-1) + (\kappa+1)p_3/p_1 } > \frac{\ensuremath{\mathit{V}}_c} { (\kappa_c - 1) + (\kappa_c+1)p_3/p_1} ,$$ (28.19)

which is very similar to eq.(27.7). In the same fashion, under the assumption that the polytropic indexes are of the same order of magnitude, eq.(28.19) implies $\ensuremath{\mathit{V}}_c\!<\!\ensuremath{\mathit{V}}_1$, which was an initial assumption. Although eq.(28.19) is not sufficient, because $\ensuremath{\mathit{V}}_c$ is a first order quantity, we can use in what follows:

$$\ensuremath{v}_2 > \ensuremath{v}_c.$$ (28.20)

The inequalities in eq.(28.17) and eq.(28.20) will prove to be useful later when we choose a more suitable reference system to describe the problem in question.