§25 Curved jets

Let us now use the results obtained in sections §23 and §24 and apply them to the case of jets that are curved due to any mechanism, for example the interaction of the jet with a cloud as was discussed in Chapter III.

The greatest danger occurs when a jet is bent and forms internal shock waves. This is because, after a shock, the normal velocity component of the flow to the surface of the shock becomes subsonic and the jet flares outward. Nevertheless, as we have seen in section §24, the shock that forms when gas flows around a curved profile (such as a bent jet due to external pressure gradients) does not start from the boundary of the jet. It actually forms at an intermediate point to the flow. In other words, it is possible that, if a jet does not bend too much the intersection of the characteristic lines actually occurs outside the jet and the flow can curve without the production of internal shocks.

As we have seen in section §24 the Mach angle of the flow, relativistic and non-relativistic, does not remain constant in the bend -see for example eq.(24.7) and eq.(24.10). The Mach number monotonically decreases as the bend proceeds.

Eq.(24.7) and eq.(24.10) imply that:

$$\tan \alpha = - \mu \cot \mu \left( \alpha + \theta - \phi_* \right).$$ (25.1)

where

$$\mu \equiv \begin{cases}\sqrt{ ( \kappa - 1 ) / ( \kappa + 1 ) } ... ...}, \ \sqrt{ \kappa - 1 } & \text{ for an ultrarelativistic gas. } \end{cases}$$ (25.2)

As was mentioned above, if the jet is sufficiently narrow, it appears that it can safely avoid the formation of an internal shock. However, differentiation of eq.(25.1) with respect to the angle the velocity vector makes with the $x$ axis, that is the deflection angle $\theta$, implies that:

$$\frac{ \mathrm{d} \alpha }{ \mathrm{d} \theta } = \frac{ 1 }{ 2 } \left( \Gamma - 1 + \frac{ \Gamma + 1 }{ M^2 - 1 } \right),$$ (25.3)

with

$$\Gamma \equiv \begin{cases}\kappa & \text{ if the gas is classica... ...\ \kappa / ( 2 - \kappa ) & \text{ for an ultrarelativistic gas.} \end{cases}$$ (25.4)

The Mach number $M$ is given by eq.(11.22) and eq.(11.20) respectively. As the Mach number $M \! \rightarrow 1$, then the derivative $\mathrm{d} \alpha / \mathrm{d} \theta \rightarrow \! \infty$. This means that the rate of change of the Mach angle with respect to the deflection angle grows without limit as the Mach number decreases and reaches unity. On a bend, the Mach number decreases and care is needed, otherwise characteristics will intersect at the end of the curvature. There is only one special shape for which this effect is bypassed and this occurs when the increase of $\theta$ matches exactly with the increase of $\alpha$ (Courant & Friedrichs, 1976), but of course, this is quite a unique case. It appears however, that whatever the thickness of the jet it cannot be bent more than the point at which $\mathrm{d} \alpha / \mathrm{d} \theta$ exceeds the rate of change of $\theta$ with respect to the bending angle $\theta$. In other words, $\mathrm{d} \alpha / \mathrm{d} \theta \! \le \! \mathrm{d} \theta / \mathrm{d} \theta \! = \! 1$. From this last inequality and eq.(25.3) a value of the Mach number can be obtained (Icke, 1991):

$$M_\star = \frac{ 2 }{ \sqrt{ 3 - \Gamma } }.$$ (25.5)

If the Mach number in the jet decreases in such a way that the value $M_\star$ is reached, then a terminal shock is produced and the jet structure is likely to be disrupted. It is important to note that this terminal shock is weak since $M \! \gtrsim \! 1$ and so, it might not be too disruptive. Nevertheless, this monotonic decrease of the Mach number makes the jet to flare outwards, even if the terminal shock is weak.

Let us now calculate an upper limit for the maximum deflection angle for which jets do not produce terminal shocks. In order to do so, we rewrite eq.(25.1) in the following way:

$$- \theta = \arcsin \frac{ 1 }{ M } + \frac{1}{\mu} \arctan \left\{ \mu \sqrt{ M^2 - 1 } \right\} - \phi_*$$ (25.6)

To eliminate the constant $\phi_*$ from all our relations, we can compare the angle $\theta$ evaluated at the minimum possible value of the Mach angle $M \! = \! M_\star$ with $\theta$ evaluated at its maximum value $M \! = \! \infty$. In other words, the angle $\theta_{\text{max}}$ defined as:

$$\theta_{\text{max}} \equiv \theta ( M \! = \! M_\star ) - \theta ... ... \unit{ 47.94 }{ \degree } & \text{ for an ultrarelativistic gas. } \end{cases}$$ (25.7)

is an upper limit to the deflection angle. Jets which bend more than this limiting value $\theta_{\text{max}}$ develop a terminal shock and the jet will flare outward.

This upper limit however, does not mean that the jet is immune from developing an internal shock if it is bent by a smaller angle. Indeed, let us suppose that the jet bends and that the curvature it follows is a segment of a circle as it is shown in fig.(IV.3). According to the figure, the equation of the characteristic OA that emanates from the point O, where the curvature starts is:

$$y = x \tan \alpha$$ (25.8)

Figure IV.3: Sketch of a curved jet of radius $D$ that develops a shock at the beginning of the curvature. The curve is assumed to be a circle with radius $R$. The Mach angle of the jet is $\alpha$ at the left of the characteristic OA that emanates from the point where the bending starts.

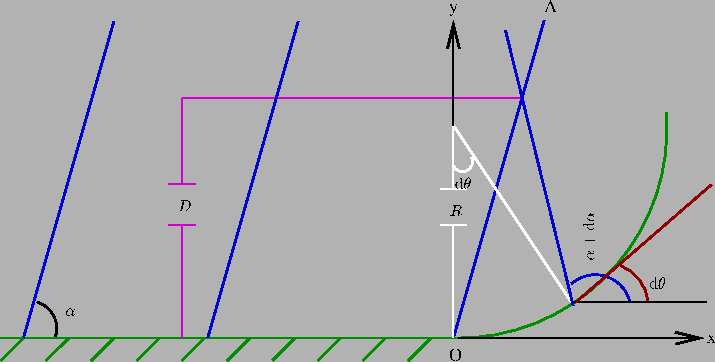
Once the flow has curved $\mathrm{d} \theta$ degrees, the characteristic at this point is given by:

$$\begin{split} y & = ( x - R \mathrm{d} \theta ) \tan ( \alpha + \... ...thrm{d} \theta ) / \cos^2 \alpha - R \mathrm{d} \theta \tan \alpha, \end{split}$$

where R is the radius of curvature of the circular trajectory. The intersection of this characteristic and that given by eq.(25.8) occurs when the $y$ coordinate has a value:

$$D = \frac{ R \sin^2 \alpha }{ 1 + \mathrm{d} \alpha / \mathrm{d} \theta }.$$

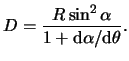
Substitution of eq.(25.3) gives (Icke, 1991):

$$\frac{ D }{ R } = \frac{ 2 }{ \Gamma + 1 } \left( M^2 - 1 \right) M^{-4}.$$ (25.9)

Using eq.(25.6) and eq.(25.9) it is possible to make a plot in which two zones separate the cases for jets which develop shocks at the onset of the curvature, and the ones that do not. Indeed, we can plot the ratio of the width of the jet $D$ to radius of curvature $R$ as a function of the difference $\theta - \theta_\star$ between the deflection angle $\theta$ and the maximum deflection angle $\theta_\star \! \equiv \! \theta( M_\star )$, as is shown in fig.(IV.4).

Jets for which the ratio $D / R$ lies below the curve do not develop any shocks at all. For example, consider a jet with a given Mach number for which its ratio $D / R$ is given. As the width of the jet increases (or the radius of curvature of the profile decreases), it comes a point in which a shock at the onset of the curvature is produced. In the same way, jets with a fixed ratio $D / R$ for a given Mach number which are initially stable -so that they lie below the curve- can develop a shock at the beginning of the curvature by increasing the bending angle of the curve.

Figure IV.4: Plot of the maximum ratio $D / R$ as a function of the difference $\theta - \theta_\star$ where $\theta$ is the deflection angle and $\theta_\star$ is the maximum bending angle a jet can have in order not to produce a terminal shock. The plot refers to the points for which a shock at the beginning of the curvature (which was assumed to be a circle) has developed. Jets with parameters which lie below the curve in any case do not develop any internal shocks at all for this particular circular trajectory. The plot at the top was calculated using the results in which the gas is classical and its polytropic index is $5/3$. The plot at the bottom was made by considering the gas to be ultrarelativistic and relativistic effects in the bulk motion of the flow were taken into account. For this second plot, the polytropic index was assumed to be $4/3$. The numbers in every plot correspond to the values of the Mach number in the flow.

The relativistic Mach angle is smaller for a given value of the velocity of the flow than its classical counterpart as it was proved in Section §11 -see for example fig.(II.2). This fact is extremely important when analysing the possibility of the intersection of different characteristics in a jet that bends. For a relativistic flow, the characteristics, which make an angle equal to the Mach angle to the streamlines, are always beamed in the direction of the flow. Thus, when a jet starts to bend the possibility of intersection between some characteristic line in the curved jet and the ones before the flow has curved, become more probable than their classical counterpart.

This difference results in a severe overestimation of the maximum bending angle $\theta_{\text{max}}$. For example, Icke (1991) used the classical analysis in the discussion of the generation of internal shocks due to bending of jets. Using the classical equations described above, but with a polytropic index $\kappa = 4 / 3$, then $\theta_{\text{max}} \! = \! \unit{134.16}{\degree}$. This is much greater than the value of $\theta_{\text{max}} \! = \unit{74.21}{\degree}$ obtained with a full relativistic treatment which is impossible.

The analysis made by Icke (1991) is important for jets in which the microscopic motion of the flow inside the jet is relativistic, but the bulk motion of the flow is non-relativistic.