Next: §24 Steady simple waves Previous: IV Stability of non-straight Contents
Let us describe briefly the exact solution of the equations of
hydrodynamics for plane steady flow depending on one angular variable
![]() only. This problem was first investigated by Prandtl and
Meyer in 1908 (Courant & Friedrichs, 1976; Landau & Lifshitz, 1995) for the case in which relativistic
effects were not taken into account. The full relativistic solution to
the problem is due to Kolosnitsyn & Stanyukovich (1984).
only. This problem was first investigated by Prandtl and
Meyer in 1908 (Courant & Friedrichs, 1976; Landau & Lifshitz, 1995) for the case in which relativistic
effects were not taken into account. The full relativistic solution to
the problem is due to Kolosnitsyn & Stanyukovich (1984).
For this case, Euler's equation, eq.(9.6) and the continuity equation, eq.(9.1) can be written:
where
![]() and
and ![]() are the components
of the velocity in the radial and azimuthal directions respectively.
Eq.(23.3) is the Bernoulli equation, eq.(9.8), for
this problem.
are the components
of the velocity in the radial and azimuthal directions respectively.
Eq.(23.3) is the Bernoulli equation, eq.(9.8), for
this problem.
Using the definition of the speed of sound, eq.(11.3), in eq.(23.2) with the aid of eq.(23.3) it is found that:
On the other hand, differentiation of
![]() with
respect to the azimuthal angle
with
respect to the azimuthal angle ![]() and using eq.(23.3),
gives:
and using eq.(23.3),
gives:
Multiplication of eq.(23.4) by
![]() and
substracting this from eq.(23.5) gives:
and
substracting this from eq.(23.5) gives:
On the other hand, Bernoulli's equation, eq.(23.3), together with the value of the specific enthalpy for a polytropic gas given in eq.(12.4), can be rewritten
in which it has been assumed that at some definite point,
the flow velocity vanishes and the speed of sound has a value ![]() there. It is always possible to make the velocity zero at a certain
point by a suitable choice of the system of reference.
there. It is always possible to make the velocity zero at a certain
point by a suitable choice of the system of reference.
Eqs.(23.6)-(23.7) can be solved in terms of
![]() and
and ![]() :
:
Because
![]() , eq.(23.1) gives the required solution (Kolosnitsyn & Stanyukovich, 1984):
, eq.(23.1) gives the required solution (Kolosnitsyn & Stanyukovich, 1984):
This equation gives the speed of sound as a function of the
azimuthal angle. From eqs.(23.8)-(23.9) it follows that
the radial and azimuthal velocities can be obtained as a function of the
same angle ![]() . Because of this, all the remaining hydrodynamical
variables can be found. The sign in eq.(23.11) can be chosen
to be negative by measuring the angle
. Because of this, all the remaining hydrodynamical
variables can be found. The sign in eq.(23.11) can be chosen
to be negative by measuring the angle ![]() in the appropriate
direction and we will do that in what follows.
in the appropriate
direction and we will do that in what follows.
Let us consider now the case of an ultrarelativistic gas and integrate eq.(23.11) by parts, to obtain:
For the case of an ultrarelativistic gas, the speed of sound
![]() is given by eq.(12.6). In other words, this velocity is
constant and so the integral in eq.(23.12) is a Lebesgue integral.
Since this integral is taken over a bounded and measurable function over
a set of measure zero, its value is zero.
is given by eq.(12.6). In other words, this velocity is
constant and so the integral in eq.(23.12) is a Lebesgue integral.
Since this integral is taken over a bounded and measurable function over
a set of measure zero, its value is zero.
Using eqs.(23.8)-(23.9) and eq.(23.12) the desired solution is obtained (Kolosnitsyn & Stanyukovich, 1984; Königl, 1980):
for an ultrarelativistic equation of state of the gas.
For the classical case, in which
![]() ,
eq.(23.11) gives for a polytropic gas with polytropic index
,
eq.(23.11) gives for a polytropic gas with polytropic index ![]() :
:
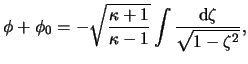 |
|
|
where
| |
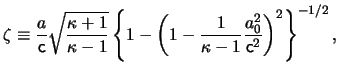 |
|
|
and so, the required solution is (Kolosnitsyn & Stanyukovich, 1984):
| |
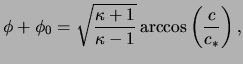 |
(23.15) |
where the speed of sound ![]() has been rewritten as
has been rewritten as ![]() to be consistent in the non-relativistic case. The critical
velocity of sound
to be consistent in the non-relativistic case. The critical
velocity of sound ![]() is given by (Landau & Lifshitz, 1995):
is given by (Landau & Lifshitz, 1995):
The value for the velocities can thus be calculated from
eq.(23.1) and eq.(23.9) with
![]() :
:
Some important inequalities must be satisfied for the flow under
consideration. First of all, eq.(23.11) together with
eq.(12.4) and the first law of thermodynamics imply that
![]() . Using this inequality
and the fact that
. Using this inequality
and the fact that
![]() combined with the first law of thermodynamics, it follows
that
combined with the first law of thermodynamics, it follows
that
![]() . Also, using
eqs.(23.8)-(23.9) it follows that
. Also, using
eqs.(23.8)-(23.9) it follows that
![]() and
necessarily
and
necessarily
![]() .
.
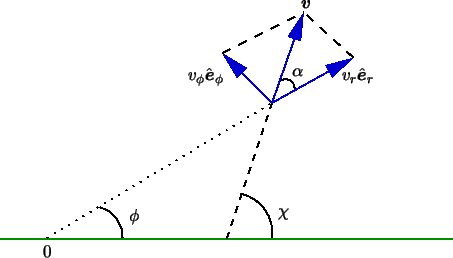
On the other hand, the angle ![]() that the velocity vector makes
with a definite axis is related to the velocity and the azimuthal angle
that the velocity vector makes
with a definite axis is related to the velocity and the azimuthal angle ![]() by:
by:
as it is seen from fig.(IV.1). Thus, since the ![]() component of Euler's equation, eq.(9.6) implies that:
component of Euler's equation, eq.(9.6) implies that:
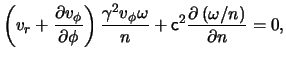
it follows that
![]() .
.
|
In other words, we have proved that for the flow for which we are concerned, the following inequalities are satisfied:
A flow with these properties is often described as a rarefaction wave (Landau & Lifshitz, 1995) and we will use this name in what follows.
Another, very important property of this rarefaction wave is
that the lines at constant ![]() intersect the streamlines at
the Mach angle, that is, they are characteristics. Indeed, from
fig.(IV.1), it follows that the angle
intersect the streamlines at
the Mach angle, that is, they are characteristics. Indeed, from
fig.(IV.1), it follows that the angle ![]() between the
line
between the
line
![]() and the velocity vector
and the velocity vector
![]() is given by
is given by
![]() .
Using eqs.(23.8)-(23.10) it follows that this relation can
be written as eq.(11.20). Because all quantities in the problem
are functions of a single variable, the angle
.
Using eqs.(23.8)-(23.10) it follows that this relation can
be written as eq.(11.20). Because all quantities in the problem
are functions of a single variable, the angle ![]() , it follows
that every hydrodynamical quantity is constant along the characteristics.
, it follows
that every hydrodynamical quantity is constant along the characteristics.
Sergio Mendoza Fri Apr 20, 2001