§9 Equations of motion in relativistic fluid dynamics

The conservation of mass in the absence of any sinks or sources is described by the relativistic continuity equation (Landau & Lifshitz, 1995):

$$\frac{ \partial n^k }{ \partial x^k } = 0,$$ (9.1)

where the particle flux 4-vector $n^k \! = \! n u^k$ and the scalar $n$ is the proper number density of particles in the fluid. The energy-momentum tensor in eq.(8.4) does not take into account any dissipative processes and therefore the equations of motion expressed by eq.(8.1) refer to an ideal fluid.

We now project eq.(8.1) on the direction of the 4-velocity, that is, we multiply eq.(8.1) by $u^i$ and use the fact that $u^i u_i \! = \! 1$ which implies

$$nu^k\left\{ \frac{ \partial }{ \partial x^k } \left( \frac{ \omeg... ...n } \right) - \frac{ 1 }{ n } \frac{ \partial p }{ \partial x^k } \right\} = 0.$$ (9.2)

By the first law of thermodynamics:

$$\mathrm{d}\left( \omega / n \right) = T \mathrm{d} \left( \sigma / n \right) + \left( 1 / n \right) \mathrm{d} p,$$ (9.3)

in which $T$ is the temperature and $\sigma$ the entropy per unit volume, together with the continuity equation, eq.(9.1), it follows that eq.(9.2) can be rewritten as:

$$u^k \frac{ \partial }{ \partial x^k } \left( \frac{ \sigma }{ n }... ... \mathrm{d} }{ \mathrm{d} \mathit{s} } \left( \frac{ \sigma }{ n } \right) = 0,$$ (9.4)

where the derivative $\mathrm{d} / \mathrm{d} \mathit{s}$ means differentiation along the world line $s$ of the fluid element concerned and the interval $\mathrm{d} \mathit{s}^2 = g_{ik} \mathrm{d} x^i \mathrm{d} x^k$. Eq.(9.4) means that the fluid is adiabatic.

Let us now project eq.(8.1) on a direction orthogonal to $u^i$. To do so, note that the tensor $\left\{ \delta_i^l - u_i u^l \right\}$ is perpendicular to $u^i$. We can multiply eq.(8.1), that is $\partial T_l^k / \partial x^k \! = \! 0$, by this tensor and find

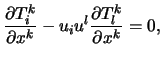$$\frac{ \partial T_i^k }{ \partial x^k } - u_i u^l \frac{ \partial T_l^k }{ \partial x^k } = 0,$$ (9.5)

which is indeed a perpendicular vector to $u^i$. Expansion of this relation results in the equation:

$$\omega u^k \frac{ \partial u_i }{ \partial x^k } = \frac{ \partial p }{ \partial x^i } - u_i u^k \frac{ \partial p }{ \partial x^k },$$ (9.6)

which is the 4-dimensional Euler equation. The three spatial components constitute the relativistic Euler equation:

$$\frac{ \gamma \omega }{ \ensuremath{\mathsf{c}}^2 } \left\{ \frac... ...l{\mathit{v}} }{ \ensuremath{\mathsf{c}}^2 } \frac{ \partial p }{ \partial t} ,$$ (9.7)

where $\boldsymbol{\mathit{v}}$ is the flow velocity and the Lorentz factor $\gamma$ is given by $\gamma = 1 / \sqrt*( 1 - \ensuremath{v}^2/\ensuremath{\mathsf{c}}^2)$. The time component of eq.(9.6) is implied by the other three. In the case of isentropic flow, that is, when $\sigma / n \! = \! \mathrm{const}$, and assuming the flow to be steady, the spatial components of eq.(9.6) give

$$\gamma \left( \boldsymbol{\mathit{v}} \cdot \boldsymbol{\mathrm{g... ...remath{\mathsf{c}}^2 \boldsymbol{\mathrm{grad}} \left( \omega / n \right) = 0.$$

Scalar multiplication by $\boldsymbol{\mathit{v}}$ leads to $( \boldsymbol{\mathit{v}} \cdot \boldsymbol{\mathrm{grad}} ) ( \gamma \omega / n ) = 0$ which implies that along any streamline the quantity

$$\gamma \omega / n = \mathrm{const}.$$ (9.8)

This is the relativistic version of Bernoulli's equation.

Footnotes

... equation.

Bernoulli's equation is also obtained directly from the time component of eq.(9.6) when the flow is steady and isentropic. The result is $\gamma ( \boldsymbol{\mathit{v}} / \ensuremath{\mathsf{c}}) \cdot \boldsymbol{\mathrm{grad}} ( \omega \gamma / n ) \! = 0$, which is equivalent to eq.(9.8).