§11 Characteristics

Let us consider now the one dimensional problem of a relativistic flow in which dissipation processes are not taken into account, that is, the entropy remains constant as the fluid moves. For this particular case, the continuity equation, eq.(9.1) and the $x$-component of the equations of motion, eq.(8.1) are given by:

$$\frac{ \partial }{ \partial t} \left( \gamma n \right) + \frac{ \partial }{ \partial x } \left( \gamma n \ensuremath{v}\right) = 0,$$ (11.1)
and

$$\frac{ 1 }{ \ensuremath{\mathsf{c}}^2 } \frac{ \partial }{ \parti... ...\omega \ensuremath{v}^2 \gamma^2 }{ \ensuremath{\mathsf{c}}^2 } - P \right) = 0$$ (11.2)

respectively. If we define the quantities:

$$\alpha \equiv \frac{ a }{ \ensuremath{\mathsf{c}}} \equiv \left( \frac{ \partial P }{ \partial e } \right)_\sigma,$$ (11.3)

$$\varphi \equiv \frac{ 1 }{ \ensuremath{\mathsf{c}}} \int{ \frac{ a }{ n } \mathrm{ d } n },$$ (11.4)

then eq.(11.1) and eq.(11.2) can be written as:

$$\left( 1 - \frac{ \ensuremath{v}^2 }{ \ensuremath{\mathsf{c}}^2 }... ...{v}}{ \partial t } + \frac{ \partial \ensuremath{v}}{ \partial x} \right\} = 0,$$ (11.5)

$$\alpha \left( 1 - \frac{ \ensuremath{v}^2 }{ \ensuremath{\mathsf{... ...{ \ensuremath{\mathsf{c}}^2 } \frac{ \partial \ensuremath{v}}{ \partial x} = 0.$$ (11.6)

Addition and substraction of these two relations gives:

$$\mathcal{D}_\pm \left( \frac{ \ensuremath{v}}{ \ensuremath{\maths... ...remath{v}^2 }{ \ensuremath{\mathsf{c}}^2 } \right) \mathcal{D}_\pm \varphi = 0,$$ (11.7)
where:

$$\mathcal{D}_\pm f \equiv \left( 1 \pm \alpha \frac{ \ensuremath{v... ...remath{v}}{ \ensuremath{\mathsf{c}}} \right) \frac{ \partial f }{ \partial x },$$ (11.8)

for any function $f(t,x)$. From the definitions of the operator $D_{\pm}$ in eq.(11.8), it follows that:

$$\frac{ \mathcal{D}_{\pm} \left( \ensuremath{v}/ \ensuremath{\math... ...\mathsf{c}}}{ 1 - \ensuremath{v}/ \ensuremath{\mathsf{c}}} \right\}^{ 1 / 2 },$$

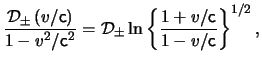
and hence, eqs.(11.7) become:

$$\left( 1 - \ensuremath{v}^2 / \ensuremath{\mathsf{c}}^2 \right) \... ... 1 - \ensuremath{v}/ \ensuremath{\mathsf{c}}} \right) \pm \varphi \right\} = 0.$$ (11.9)

If we now introduce the parameters:

$$\mathcal{J}_\pm \equiv \varphi \pm \ln\left\{ \frac{ 1 + \ensurem... ...{\mathsf{c}}}{ 1 - \ensuremath{v}/ \ensuremath{\mathsf{c}}} \right\}^{ 1 / 2 },$$ (11.10)

which are called Riemann invariants, then eqs.(11.9), that is, eqs.(11.1)-(11.2), become equivalent to (Taub, 1948; Taub, 1978):

$$\left[ \left( 1 \pm \alpha \frac{ \ensuremath{v}}{ \ensuremath{\m... ...athsf{c}}} \right) \frac{ \partial }{ \partial x } \right] \mathcal{J}_\pm = 0.$$ (11.11)

From this relation it follows that the Riemann invariants $\mathcal{J}_\pm$ are constant along the curves $\mathrm{d} x / \mathrm{d} t \! = \! \pm c ( \alpha \pm \ensuremath{v}/ \ensuremath{\mathsf{c}}) / ( 1 \pm \alpha \ensuremath{v}/ \ensuremath{\mathsf{c}})$ respectively. These curves $\mathcal{C}_\pm$ are called characteristics and play an essential role in fluid dynamics. The differential operators that appear inside the brackets in eq.(11.11) are the operators of differentiation along the characteristics $\mathcal{C}_\pm$ in the $x$   -$t$ plane.

In general terms, a disturbance is said to propagate as a travelling wave (Taub, 1948; Landau & Lifshitz, 1995) if either $\mathcal{J}_+$    or $\mathcal{J}_-$ is constant. For instance, consider the case in which $\mathcal{J}_- \! = \! \mathrm{ const }$, then from eq.(11.10), and eq.(11.11) it follows that (Taub, 1948):

$$\frac{ 1 }{ \ensuremath{\mathsf{c}}} \frac{ \partial \varphi }{ \partial t } + \Psi(\varphi) \frac{ \partial \varphi }{ \partial x } = 0,$$ (11.12)
with

$$\Psi(\varphi) \equiv \frac{ \alpha + \ensuremath{v}/ \ensuremath{\mathsf{c}}}{ 1 + \alpha \ensuremath{v}/ \ensuremath{\mathsf{c}}}.$$ (11.13)

The general solution of eq.(11.12) is

$$f(\varphi) = x - \Psi(\varphi) \ensuremath{\mathsf{c}}t$$ (11.14)

in which $f(\varphi)$ is an arbitrary function. The relation eq.(11.14) means that $\varphi$ is constant along straight lines with slope $\Psi(\varphi)$ in the plane $x$   -$\ensuremath{\mathsf{c}}t$. In other words, $\Psi(\varphi)$ is the velocity of propagation of $\varphi$. From the definition of $\Psi$ in eq.(11.13) it follows that, for weak disturbances in which $\ensuremath{v}\! \rightarrow \! 0,$    then $\Psi(\varphi) \! \rightarrow \alpha$.

The speed of sound is the velocity at which adiabatic perturbations of small amplitude in a compressible fluid move with respect to the flow. Due to the fact that $\Psi(\varphi) \! \rightarrow \alpha$    as $\ensuremath{v}\! \rightarrow \! 0$, it is obvious that $\alpha$ represents the speed of sound in units of the speed of light.

The properties of subsonic and supersonic flow, that is flow with velocity less or greater than that of sound, are completely different in nature. To begin with, let us see how perturbations with small amplitudes are propagated along the flow for both, subsonic and supersonic flows. For simplicity in the following discussion we will consider two dimensional flow only. The relations obtained below are easily generalised for the general case of three dimensions.

If a gas in a steady motion receives a small perturbation, this propagates through the gas with the velocity of sound relative to the flow itself. In another system of reference, the laboratory frame, in which the velocity of the flow is $\ensuremath{v}$ along the $x$ axis, the perturbation travels with an observed velocity $\boldsymbol{u}$ whose $x$    and $y$ components are given by:

$$u_x = \frac{ a \cos\theta + \ensuremath{v}}{ 1 + a \ensuremath{v}\cos\theta / \ensuremath{\mathsf{c}}^2 },$$ (11.15)

$$u_y = \frac{ \gamma^{-1} a \sin\theta }{ 1 + a \ensuremath{v}\cos\theta / \ensuremath{\mathsf{c}}^2 },$$ (11.16)

according to the rule for the addition of velocities in special relativity (Landau & Lifshitz, 1994a). The polar angle $\theta$ and the velocity of sound $a$ are both measured in the proper frame of the fluid. Since a small disturbance in the flow moves with the velocity of sound in all directions, the parameter $\theta$ can have values $0 \! \le \! \theta \! \le \! 2 \pi$. This is illustrated pictorially in fig.(II.1).

Figure II.1: Region of influence of small amplitude perturbations. A perturbation of small amplitude is produced in the flow at some point $0$. This is carried by the flow which has a velocity $\boldsymbol{\ensuremath{v}}$. In the case of subsonic flow, as shown in panel (a), the perturbation is able to propagate to the whole space. When the flow is supersonic the perturbation is propagated only downstream inside a cone with aperture angle $2 \alpha$. The speed of sound $a$ and the angle $\theta$ are measured in a frame of reference in which the flow is at rest -the proper frame of the flow. The vector $\boldsymbol{u}$ is the relativistic addition of vectors $\boldsymbol{\ensuremath{v}}$    and $a \hat{ \boldsymbol{ e } }_r'$, where $\hat{ \boldsymbol{e} }_r'$ is a unit radial vector in the proper frame of the flow.

Let us consider first the case in which the flow is subsonic, as is presented in case (a) of fig.(II.1). Since by definition $\ensuremath{v}\! < \! a$ and $\ensuremath{\mathsf{c}}^2 > a \ensuremath{v}$, it follows from eqs.(11.15)-(11.16) that $u_x( \theta \! = \! \pi ) \! < \! 0$    while $u_y( \theta \! = \! \pi ) \! = \! 0$. In other words, the region influenced by the perturbation contains the velocity vector $\boldsymbol{\ensuremath{v}}$. This means that the perturbation originating at $0$ is able to be transmitted to all the flow.

When the velocity of the flow is supersonic, the situation is quite different, as shown in case (b) of fig.(II.1). For this case it follows that $u_x( \theta \! = \! \pi ) \! > \! 0$    and $u_y( \theta \! = \! \pi ) \! = \! 0$. In other words, the velocity vector $\boldsymbol{\ensuremath{v}}$ is not fully contained inside the region of influence produced by the perturbation. This implies that only a bounded region of space will be influenced by the perturbation originated at position $0$. For the case of steady flow, this region is evidently a cone. Thus, a disturbance arising at any point in supersonic flow is propagated only downstream inside a cone of aperture angle $2 \alpha$. By definition, the angle $\alpha$ is such that it is the angle subtended by the unit radius vector $\hat{ \boldsymbol{e} }_r$ with the velocity vector $\boldsymbol{\ensuremath{v}}$ at the point in which the azimuthal unit vector $\hat{ \boldsymbol{e} }_\alpha$ is orthogonal with the tangent vector $\mathrm{d} ( a \hat{ \boldsymbol{e} }_r' ) / \mathrm{d} \theta$ to the boundary of the region influenced by the perturbation. The unit vector $\hat{ \boldsymbol{e} }_r'$ is the unit radial vector in the proper frame of the flow. In other words, the angle $\alpha$ obeys the following mathematical relation:

$$\frac{ \mathrm{d} \left( a \hat{ \boldsymbol{e} }_r' \right) }{ \mathrm{d} \theta } \cdot \hat{ \boldsymbol{e} }_\alpha = 0.$$ (11.17)

Substitution of eqs.(11.15)-(11.16) into eq.(11.17) gives:

$$\tan \alpha = - \gamma \left\{ \frac{ 1 }{ \tan \theta } + \frac{ a \ensuremath{v}}{ \ensuremath{\mathsf{c}}^2 \sin \theta } \right\} .$$ (11.18)

On the other hand, since $\tan \alpha \! = \! u_y / u_x$, it follows from eqs.(11.15)-(11.16) and eq.(11.18) that:

$$\tan \theta = - \frac{ \ensuremath{v}}{ a } \sqrt{ 1 - \frac{ a^2 }{ \ensuremath{v}^2 } } ,$$

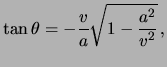
so eq.(11.18) gives a relation between the angle $\alpha$, the velocity of the flow $\ensuremath{v}$ and its sound speed $a$:

$$\tan \alpha = \gamma^{-1} \frac{ a / \ensuremath{v}}{ \sqrt{ 1 - \left( a / \ensuremath{v}\right)^2 } }$$ (11.19)

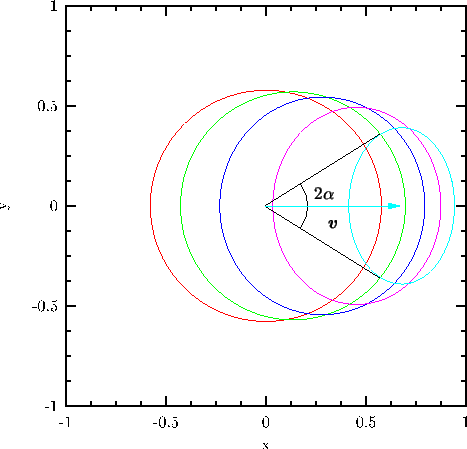
This variation of the angle $\alpha$ is plotted in fig.(II.2) for the case in which the gas is assumed to have a relativistic equation of state, that is, when $p \! = \! e / 3$. The important feature to note from the plot is that the aperture angle of the cone of influence is reduced when the velocity of the flow approaches that of light.

From eq.(11.19) it follows that, as the velocity of the flow approaches that of light, the angle $\alpha$ vanishes. In other words, as the velocity reaches its maximum possible value, the perturbation is communicated in a very narrow region along the velocity of the flow.

In studies of supersonic motion of fluid mechanics it is very useful to introduce a dimensionless quantity $M$ defined as:

$$\frac{ 1 }{ M } \equiv \sin \alpha = \frac{ \gamma_a }{ \gamma } \frac{ a }{ \ensuremath{v}},$$ (11.20)

according to eq.(11.19). The quantity $\gamma_a \equiv \! 1 / \sqrt{ 1 - ( a / \ensuremath{\mathsf{c}})^2 }$ is the Lorentz factor for the velocity of sound $a$. The number $M$ has the property that $M \! \rightarrow \! 1$    as $\ensuremath{v}\! \rightarrow \! a$    and $M \! \rightarrow \! \infty$    as $\ensuremath{v}\! \rightarrow \ensuremath{\mathsf{c}}$. It also follows that $M \! > \! 1$ if and only if $\ensuremath{v}\! > \! a$.

Figure II.2: Region of influence of a perturbation for different values of the velocity of a relativistic gas with a sound speed $a \! = \ensuremath{\mathsf{c}}/ \sqrt*{3}$. From left to right the closed loops correspond to values of the velocity $\ensuremath{v}$ of $0.0,\ 0.2, 0.4,\ldots ,0.8$ in units of the speed of light $\ensuremath{\mathsf{c}}$. The perturbation is assumed to originate at the origin of the proper system of reference of the flow. In the case of supersonic flow, the region of influence occurs only downstream inside a cone with aperture angle $2 \alpha$. This cone surrounds the corresponding loop and is tangent to it. When the flow is subsonic, the perturbation is transmitted to all the flow. As a particular example, the cone and the velocity vector have been drawn for the case in which the velocity is $\ensuremath{v}\! = \! 0.8 \ensuremath{\mathsf{c}}$.

The surface bounding the region reached by a disturbance starting from the origin $0$ is called a characteristic surface (Landau & Lifshitz, 1995). This definition of characteristic and that given above, when the Riemann invariants were introduced, are the same in the sense that the characteristics introduced here are curves in the $x$   -$y$ plane which cut the streamlines in this plane at the Mach angle. Those discussed above correspond to curves in the $x$   -$t$ plane which cut the streamlines (that is, the curves $x(t)$ for which $\mathrm{d} x / \mathrm{d} t \! = \! \ensuremath{v}$) at the Mach angle in this plane.

In the general case of arbitrary steady flow, the characteristic surface is no longer a cone. However, exactly as it was shown above, the characteristic surface cuts the streamlines at any point at the angle $\alpha$.

One of the main differences between supersonic and subsonic flow is the possibility of a certain type of discontinuities in the flow, called shock waves. For example, from eq.(11.14) it follows that for certain functions $f(\varphi)$, which are determined by the particular boundary conditions of the problem in question, the curves $\varphi \! = \! \mathrm{const}$ in the $x$   -$t$ plane intersect. Since the Riemann invariants as defined in eq.(11.10) are constant along these curves, with a different constant for each curve, it follows that for travelling waves the velocity $\ensuremath{v}$ and the other hydrodynamical variables are multivalued. This is impossible in any physical circumstance and results in the creation of strong discontinuities (shock waves) on the flow.

Let us briefly discuss the classical limit of the different physical circumstances mentioned above. To do this, we make use of the relations presented in eq.(10.1) with $\ensuremath{\mathsf{c}}\! \rightarrow \! \infty$ and, as it is usual in the classical case, we represent the speed of sound by $c$.

First of all, the speed of sound $c$ is:

$$c = \left( \frac{ \partial p }{ \partial \rho } \right)^{1/2}_s.$$ (11.21)

The Riemann invariants $\mathcal{J}_\pm$ are constant along the curves $\mathrm{d} x / \mathrm{d} t \! = \! \pm ( c \pm \ensuremath{v})$. The dimensionless number $M$ satisfies the following relation:

$$\frac{ 1 }{ M } = \sin{\alpha} \xrightarrow[\ensuremath{\mathsf{c}}\rightarrow \infty]{} \frac{ \ensuremath{v}}{ c }$$ (11.22)

and is called in classical hydrodynamics the Mach number.

The results obtained about the relativistic and classical Mach number $M$ can be rewritten in the following way:

Theorem 1
The dimensionless Mach number $M$ increases without limits as the velocity of the flow takes its maximum possible value. This maximum value is the speed of light in the relativistic case and infinity in the classical case. The Mach number tends to zero as the velocity of the flow vanishes, and tends to unity as the velocity of the flow tends to the velocity of sound. This Mach number is greater than one for supersonic flow and less than unity when the velocity of the flow is subsonic.

As a way to compare the difference between the classical and relativistic Mach numbers, a plot of both of them is presented in fig.(II.3). The intersection of both curves occurs for the case in which the Mach number tends to unity, that is when the velocity of the flows tend to the local velocity of sound according to Theorem 1. For the case of subsonic flow, the relativistic Mach number is less than its classical counterpart. However for supersonic flow the relativistic Mach number is greater than the classical one.

Figure II.3: Comparison between classical and relativistic Mach numbers. The green broken line is the classical Mach number and the blue continuous curve is its relativistic analogue. The intersection of both curves occurs when the Mach number in both cases is unity, that is when the velocity of the flow $\ensuremath{v}$ is equal to the local velocity of sound. For the plot an ultrarelativistic equation of state was assumed for the gas, that is the velocity of sound $a \! = \! \ensuremath{\mathsf{c}}/ \sqrt{3}$.

Footnotes

... light

When speaking of perturbations that travel at the speed of sound with respect to the flow, we have in mind perturbations that do not involve entropy and vorticity perturbations which are transmitted with the flow itself (Landau & Lifshitz, 1995).

... number.

The relativistic generalisation of the Mach number as presented in eq.(11.20) was first calculated by Chiu (1973). This was done by reducing the problem of steady relativistic gas dynamics to an equivalent Newtonian flow and by observing that the Mach number is a pseudoscalar. From eq.(11.20) it follows that this number, the Chiu number is in fact a definition of the proper Mach number since it is defined as the ratio of the three-relativistic velocity of the flow $\gamma \ensuremath{v}$ to the three-velocity of sound $\gamma_a a$ (Königl, 1980).