§16 Initial stages of the interaction

The collision of a 2D Herbig-Haro jet with a cloud, in which the characteristic size of the cloud is much greater than the jet radius, has been studied in its initial stages by Raga & Cantó (1995). Their calculations were performed analytically and with a 2D numerical code. The analytical description of the problem was formulated as follows. Imagine a well collimated high Mach number flow (a jet) incident on a cold region of high density which is in pressure equilibrium with its surroundings (a cloud). Under the assumption that the jet radius is much smaller than the physical size of the cloud, the former can be thought as a plane parallel high density region. This assumption is essential for two reasons. First, the interaction of the jet with the cloud will result in a non significant disruption of the cloud, and second it allows a simple analytical formulation of the problem.

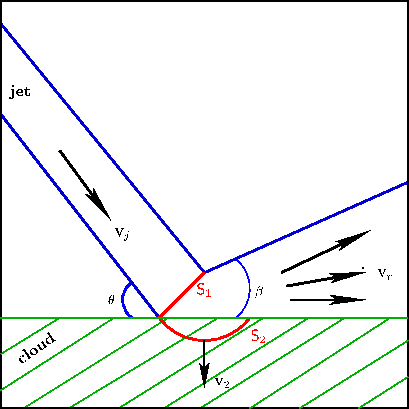
As shown in fig.(III.1), consider a jet which is incident onto a cloud at an angle $\theta$ to the plane of its surface. The interaction produces two shocks $\mathsf{S}_1$   and$\ \mathsf{S}_2$ which move with velocities $\mathprm{v}_1$   and$\mathprm{v}_2$ respectively. The shock $\mathsf{S}_1$ deflects the material in the jet to a direction parallel to the boundary of the cloud.

Figure III.1: Material within a jet travelling at velocity $\mathprm{v}_j$ collides with a dense obstacle, or cloud, which is in pressure equilibrium with its environment. The jet makes an angle $\theta$ with the tangent to the cloud before impact. The interaction produces two shocks $\mathsf{S}_1$   and$\ \mathsf{S}_2$, which move with velocities $\mathprm{v}_1$   and$\mathprm{v}_2$ respectively. The motion of $\ \mathsf{S}_2$ through the cloud starts to drill a passage through it. The interaction produces a deflection of the jet making it curve at an angle $\beta$ with respect to the cloud boundary. The velocity of the flow inside the reflected jet is $\mathprm{v}_r$.

Under the assumption that shocks $\mathsf{S}_1$   and$\ \mathsf{S}_2$ are strong, and because the pressure in the region between shocks $\mathsf{S}_1$ and $\ \mathsf{S}_2$ has to be the same, then (Raga & Cantó, 1995):

$$\mathprm{v}_2 = \sqrt{ \frac{ \rho_j }{ \rho_c } } \mathprm{v}_1,$$ (16.1)

where the uniform density of the cloud $\rho_c$ is greater than that of the density of the jet $\rho_j$. Since $\mathprm{v}_1 \leq \mathprm{v}_j$ and $\rho_j \ll \rho_c$ it follows from eq.(16.1) that $\mathprm{v}_2 \ll \mathprm{v}_j$. In other words, for a very dense cloud, the shock $\ \mathsf{S}_2$ moves into the cloud at very low velocities, causing the deformation of its boundary to occur very slowly. In the limit of very high cloud densities, it is safe to assume that the surface of the dense cloud effectively behaves as a rigid obstacle and its shape does not change as a result of the interaction (Raga & Cantó, 1995). This means that the jet is essentially interacting with a flat, rigid surface. The standard Rankine-Hugoniot conditions for a strong shock imply that the velocity of the jet after and before the collision are related to each other by:

$$\mathprm{v}_r \approx \mathprm{v}_j \cos \theta,$$ (16.2)

as can be seen from the geometry of fig.(III.1). Eq.(16.2) means that the Mach number in the jet has decreased, and in fact, it is clear from that relation that a fraction $1 - \sin^2 \theta$ of the initial kinetic energy of the jet is lost in the collision. The region behind the shock $\mathsf{S}_1$ is highly overpressured and this means that the material moving away from the region where the collision occurred expands inside a Mach cone of angle $\beta$, which is given by (Cantó et al., 1988):

$$\sin \beta \approx \frac{ 2 }{ \left( \kappa - 1 \right) M_{\textnormal{j}} \cos \theta },$$ (16.3)
where

$$M_{\textnormal{j}} = \mathprm{v_j} / c,$$ (16.4)

is the Mach number, $c$ the speed of sound and $\kappa$ the polytropic index of the flow inside the incident jet. In other words, the reflected beam looses collimation as a result of the interaction. This reduction on the collimation of the jet can be severe and could lead to a complete disruption of the jet beam. Indeed, from the conditions at the boundary of shock $\mathsf{S}_1$ it follows that the angles $\beta$ and $\theta$ are related to one another by the following relation (Cantó et al., 1988):

$$\tan \alpha = \frac{ \left( 1 - \xi \right) - \sqrt*{ \left\{ \left( 1 - \xi \right)^2 - 4 \xi \tan^2 \theta \right\} } }{ 2 \tan \theta }.$$ (16.5)
and the inverse of the compression factor tex2html_wrap_inline &xi#xi; is:

$$\xi = \frac{ \kappa - 1 }{ \kappa + 1 },$$ (16.6)

This relation has a critical value when the angle $\theta \! \equiv \! \theta_c$. The critical angle $\theta_c$ is such that for $\theta \! > \! \theta_c$ no real solutions are found and its value is:

$$\tan \theta_c = \frac{ \left( 1 - \xi \right) }{ 2 \sqrt{ \xi } } \qquad \qquad \tan \alpha_c = \sqrt{ \xi }$$ (16.7)

for a strong adiabatic shock. The critical angles in eq.(16.7) imply that for values of $\theta > \theta_c$, where:

$$\theta_c = \pi/2 - 2 \alpha_c$$ (16.8)

the flow after the $\mathsf{S}_1$ shock is subsonic (Raga & Cantó, 1995; Cantó et al., 1988). This means that the jet will not expand inside a Mach cone, but will escape from the region of the interaction between the jet and the cloud in all directions. In other words, a complete disruption to the jet has occurred.

For the case of Herbig-Haro jets in which the shock $\mathsf{S}_1$ is isothermal, (1995) made 2D numerical simulations which show the overall structure mentioned with the very simple analytical arguments mentioned above. An example of their simulation is shown in fig.(III.2).

As a short summary, what all this means is that the initial stages of a jet-cloud interaction are determined by the incidence angle $\theta$ and by the cloud to jet density ratio. This ratio determines the velocity to which the jet begins to drill a hole into the dense cloud. Whatever the final steady configuration will be, it will certainly show a jet going through a passage made by the jet as a result of the collision. If the radius of the jet is considerably smaller than the characteristic size of the cloud, the drilling of the jet through the cloud will not cause a strong effect on the overall structure of the cloud.

Eventually, the jet-cloud collision will reach a steady state in which the jet penetrates the cloud at a certain position and travels through it inside a channel drilled as a result of the interaction. The trajectory of the jet is determined by the condition that the jet maintains pressure equilibrium with the surrounding environment. In other words, as the material in the jet moves, it adjusts its pressure in such a way that it is in equilibrium with the internal pressure of the cloud.

In what follows it will be assumed that this steady configuration has been achieved by the jet as it penetrates the cloud and that its expansion takes place adiabatically. The analysis will be carried out for cases in which the material in the jet moves at non-relativistic velocities and also when it expands relativistically. In order to compare with real astronomical objects, the structure of the cloud is modelled as an isothermal gas sphere (for collisions with hydrogen clouds, most probably in the interstellar medium) and also as gas which is in pressure equilibrium within a dark matter halo (for collisions with galaxies).

Figure III.2: Two dimensional time dependent numerical simulation of a Herbig-Haro jet by Raga & Cantó (1995). A jet directed at angle $\theta \! = \! \unit{ 25 }{ \degree }$ towards the $x$-axis is injected from the left of the diagram. The cloud is in pressure equilibrium with its surroundings and its density is assumed to be $1000$ times greater than the density of the incident jet. This simulations show the presence of a shock $\ \mathsf{S}_2$ (see also fig.(III.1)) which starts to drill a hole into the cloud slowly. The initial velocity of the jet is $\mathprm{v}_j \! = \! \unit{ 100 }{ \kilo\meter \usk \reciprocal\second }$, the particle number densities of the jet, external medium and cloud are $\unit{ 5, 0.5 \text{and} 5 \times \power{ 10 }{ 2 } }{ \centi\meter\rpcubed }$ respectively. The temperatures of the corresponding regions is $\unit{ 1 \times \power{ 10 }{ 3 }, 1 \times \power{ 10 }{ 4 } \text{ and } 1 }{ \kelvin }$. Both diagrams show a time sequence of the particle number density (left) and temperature (right) stratification. The successive frames are taken at time intervals of $\unit{ 31.7 }{ yr }$ and the logarithmic contours correspond to factors of $\sqrt{ 2 }$.

Footnotes

... respectively.

Shock $\mathsf{S}_1$ is formed as a result of the interaction and is able to deflect the material of the jet at an angle $\alpha$ to the cloud. The high pressure behind this shock drives a secondary shock $\ \mathsf{S}_2$ into the cloud.