§17 Classical analysis

Once the steady state is reached, the jet penetrates the cloud and expands adiabatically. Because of this, the trajectory of the jet is determined by Euler's equation, eq.(10.6), which can be written as:

$$\hat{ \boldsymbol{\ensuremath{v}} } \left( \boldsymbol{\mathit{v}... ...at{\boldsymbol{n}} = - \boldsymbol{ \mathrm{grad} } \left( w + \phi \right),$$ (17.1)

where $w$   and$\boldsymbol{\ensuremath{v}}$ represent the heat function per unit mass and the velocity of the flow inside the jet. The gravitational forces produced by the mass of the cloud in the moving jet is given by the gradients of the gravitational potential $\phi$. The curvature $\mathsf{k}$ of the trajectory appears in the term which is proportional to its normal direction $\hat{\boldsymbol{n}}$. These two terms are proportional to the gradients of the unit tangent vector $\boldsymbol{\hat{\ensuremath{v}}}$ in the following way: $\ensuremath{v}\left( \boldsymbol{\ensuremath{v}} \cdot \boldsymbol{ \mathrm{grad} } \right) \hat{ \boldsymbol{\ensuremath{v}} } \! = \mathsf{k} \hat{n}$. From eq.(17.1) there are two equivalent ways of finding the required trajectory. The first is due to Icke (1991) and is as follows. Multiplying eq.(17.1) by the normal unit vector $\hat{\boldsymbol{n}}$ to the jet trajectory one finds:

$$\mathsf{k} \ensuremath{v}^2 = \frac{ \ensuremath{v}^2 }{ R } = - \hat{n} \cdot \boldsymbol{ \mathrm{grad} } \left( w + \phi \right),$$ (17.2)

where $R$ is the radius of curvature to the trajectory. Eq.(17.2) simply means that the normal components of the gradients of the pressure in the jet (right hand side of that equation) have to balance the centrifugal acceleration produced by the curvature of the jet (left hand side of that equation).

The second method used to find the trajectory to the jet is due to Cantó & Raga (1996) and Raga & Cantó (1996). Instead of performing scalar multiplication of eq.(17.1) with a normal vector, contraction is carried out with a tangent vector $\hat{ \boldsymbol{\ensuremath{v}} }$. This implies that $\hat{ \boldsymbol{ \ensuremath{v}} } \cdot \boldsymbol{ \mathrm{grad} } \left( \ensuremath{v}^2/2 + w + \phi \right) = 0$, that is, the path of the jet is described by Bernoulli's theorem eq.(10.7).

It is straightforward to show that if the flow in the jet is irrotational (as it is for the case we are going to consider, according to the results presented below), both relations, eq.(17.2) and Bernoulli's law are equivalent. For, if the vorticity is zero, then from the relation:

$$\boldsymbol{\ensuremath{v}} \times \boldsymbol{ \mathrm{curl} } ... ...nsuremath{v}} \cdot \boldsymbol{ \mathrm{grad} } \boldsymbol{\ensuremath{v}}$$

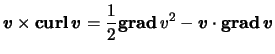
combined with Euler's equation, it follows that $\boldsymbol{ \mathrm{grad} } \left( \ensuremath{v}^2 / 2 + w + \phi \right) = 0$, which is a particular form of Bernoulli's law. Multiplication of this relation by the normal unit vector $\hat{\boldsymbol{n}}$ gives eq.(17.2). Since it is natural to work with energies, the approach by (1996) and (1996) will be used in what follows.

Let us show now that under the conditions we have previously described, the trajectory of the jet is two dimensional. From Euler's equation, it follows that the left hand side of eq.(10.6) is simply the force per unit mass experienced by a fluid particle as it moves. Since all quantities in the right hand side of that equation depend only on the distance from the cloud's centre $r$, vector multiplication of the radius vector $\boldsymbol{r}$ with eq.(10.6) implies $\mathbf{r} \! \times \! {\mathrm d} \boldsymbol{\mathit{v}}/{\mathrm d}t \! = \! 0$ . In other words, the specific angular momentum $\mathbf{l} \! = \! \mathbf{r} \! \times \! \boldsymbol{\mathit{v}}$ is conserved as the fluid moves. Since the radius vector is perpendicular to the angular momentum vector, the motion is two dimensional, and so, polar coordinates $\left( r, \varphi \right)$ are used in the following analysis.

Consider a situation in which the jet enters the cloud parallel to the $x$ axis at a distance $r_0$, so that its velocity vector is initially given by:

$$\boldsymbol{\mathit{v}}_0 = -\ensuremath{v}_0\mathbf{e}_x = -\ens... ...ft(\cos\varphi_0 \mathbf{e}_r - \sin\varphi_0 \mathbf{e}_\varphi \right),$$ (17.3)

where $\mathbf{e}_x$, $\mathbf{e}_r$ and $\mathbf{e}_\varphi$ are unit vectors in the directions $x$, $r$ and $\varphi$ respectively. Because angular momentum is conserved and the motion is two dimensional, the velocity is most simply written using eq.(17.3) as:

$$\boldsymbol{\mathit{v}} = \ensuremath{v}_r\mathbf{e}_r + \frac{r_0}{r}\ensuremath{v}_0\sin\varphi_0 \mathbf{e}_\varphi,$$ (17.4)

in which $\ensuremath{v}_r\!=\!{\mathrm d}r/{\mathrm d}t$ represents the velocity in the radial direction.

Since the steady flow of the jet expands adiabatically, we can calculate the path of the jet by means of Bernoulli's equation, eq.(10.7):

$$\frac{1}{2} \int{{\mathrm d}\ensuremath{v}^2} +\int{{\mathrm d}w} + \int{{\mathrm d}\phi} = 0,$$ (17.5)

in which the line integrals are taken from the initial position of a given fluid particle. The heat function per unit mass $w$ of the flow in the jet is given by

$$w = \Gamma^{-1} p/\rho,\Gamma \equiv (\kappa-1) / \kappa$$ (17.6)

for a gas with polytropic index $\kappa$.

Substitution of eq.(17.4) and eq.(17.3) into the first integral of eq.(17.5) gives:

$$\int{{\mathrm d}\ensuremath{v}^2} = \left\{\frac{r_0}{r} \frac{\e... ...left\{ \left(\frac{r_0}{r}\right)^2 \sin^2 \negthinspace \varphi_0 -1 \right\},$$ (17.7)

where we have used the fact that along the jet trajectory ${\mathrm d}r/\ensuremath{v}_r \! = \! r{\mathrm d}\varphi / \ensuremath{v}_\varphi$ (Landau & Lifshitz, 1995). Since the gas in the jet obeys a polytropic equation of state, we obtain for the second integral in eq.(17.5):

$$\int{{\mathrm d}w} = \frac{c_0^2}{\kappa \Gamma} \left\{ \left(\frac{p}{p_0}\right)^\Gamma - 1 \right\},$$ (17.8)

in which $c_0^2$ is the initial sound speed of the jet material. The integral for the gravitational potential produced by the self-gravitating cloud is obtained from:

$$\int{{\mathrm d}\phi} = G\int{\frac{M(r)}{r^2} {\mathrm d}r} =... ...nt{ \frac{{\mathrm d}r}{r^2} \int^r_0{\xi^2 \rho_{c}(\xi) {\mathrm d}\xi} },$$ (17.9)

where $M(r)$ and $\rho_c(r)$ represent the mass and density of the cloud at a distance $r$. Substitution of eqs.(17.8)-(17.10) into eq.(17.5) gives the relation followed by the path of the jet as it expands:

$$\begin{split}\frac{{\mathrm d}\eta}{{\mathrm d}\varphi} = \pm... ...2 \rho(\xi) {\mathrm d}\xi} }\Bigg\}^{1/2}_, \ \end{split}$$ (17.10)

in which $\eta \! = r_0 / r$ and $M_0$ is the initial Mach number of the flow in the jet. The positive and negative signs for the value of the derivative ${\mathrm d}\eta/{\mathrm d}\varphi$ in eq.(17.11) have to be chosen with care. For example, if we consider the case in which no gravity and no pressure gradients are taken into account (i.e. last two terms on the right hand side of eq.(17.11) are zero, which corresponds to a straight trajectory) the derivative ${\mathrm d}\eta/{\mathrm d}\varphi \! < \! 0$ for $\eta_* \! < \! 1 / \sin \varphi_0$ and vice versa. The equality $\eta_* \! = \! 1/ \sin\varphi_0$ corresponds to the point for which a given fluid element in the jet reaches the y axis during its motion in this particular case.

In the limit of high initial supersonic motion ( $M_0 \! \gg \! 1$) the third and fourth terms in the right hand side of eq.(17.11) are important only when $\eta \! = \! 1/\sin\varphi_0$ and we can simplify eq.(17.11) by making an expansion about this point. Indeed, in general terms, if:

$$\left( \frac{p}{p_0} \right)^\Gamma = \alpha + \beta \eta \sin\varphi_0 + \zeta \eta^2 \sin^2\negthickspace\varphi_0,$$ (17.11)
and

$$\phi - \phi_0 = 4 \pi G \left( \tilde\alpha + \tilde\beta \eta \sin\varphi_0 + \tilde\zeta \eta^2 \sin^2 \negthickspace \varphi_0 \right),$$ (17.12)

are the expansions of the pressure and gravitational potential respectively about $\eta \! = \! 1/\sin\varphi_0$, then eq.(17.11) takes the form:

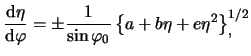$$\frac{{\mathrm d}\eta}{{\mathrm d}\varphi} = \pm \frac{1}{\sin\varphi_0} \left\{ a + b \eta + e \eta^2 \right\}^{1/2}_,$$ (17.13)
in which:

$$a \equiv 1 - \frac{2 \left( \alpha -1 \right)}{ \kappa \Gamma M_0^2 } - \frac{8\pi G}{M_0^2 c_0^2} \tilde\alpha,$$

$$b \equiv - \left( \frac{ 2 \beta }{ \kappa \Gamma M_0^2 } + \frac{8 \pi G}{M_0^2 c_0^2} \tilde\beta \right) \sin \varphi_0,$$

$$e \equiv -\left( 1 + \frac{ 2 \zeta }{ \kappa \Gamma M_0^2 } + \frac{ 8 \pi G}{M_0^2 c_0^2} \tilde\zeta \right) \sin^2 \negthinspace \varphi_0,$$

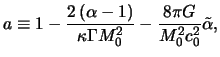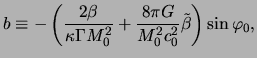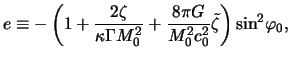to second order in $\eta \sin \varphi_0$. For the cases considered below, the general solution of eq.(17.14) is (Gradshteyn & Ryzhik, 1994):

$$\eta=\frac{1}{2e} \left\{\sqrt{\Delta}\sin\left[\sqrt{-e}\left( \... ...{\sqrt{-e}} \arcsin \frac{ 2e + b }{\sqrt{\Delta}} \right) \right] -b \right\},$$ (17.14)

with $\Delta \! \equiv \! b^2 -4ae$. The angle $\psi$ subtended between the velocity vector of the jet streamline with the $x$ coordinate axis on its way out of the cloud, the deflection angle, can be calculated from the relation $\tan\psi \! = \! (\ensuremath{v}_y/\ensuremath{v}_x)_{\text{exit}}$. In other words:

$$\psi=\arctan\left(\frac{\sin\varphi_{\mathrm e}\left({\mathrm d}\... ...\mathrm d}\varphi \right)_{\mathrm e} + \sin\varphi_{\mathrm e} }\right) + \pi,$$ (17.15)

where the subindex $e$ labels the values of different quantities at the position where the jet exits the cloud. The exit azimuthal angle $\varphi_{\mathrm e}$ is given by:

$$\varphi_e = \varphi_0 + \frac{ \sin\varphi_0 }{ \sqrt{-e} } \left\{ 2 \arcsin \frac{ 2e + b }{ \sqrt{ \Delta } } + \pi \right\},$$ (17.16)

for not very strong deflections. The derivative $( {\mathrm d}\eta / {\mathrm d}\varphi )_{\mathrm e}$ is evaluated at $\eta \! = 1$, with a negative choice of sign in eq.(17.11).