§21 Isothermal cloud and dark matter halo
As in section §18, consider the case of an isothermal cloud
being penetrated by the jet. In this case, it is possible to find an exact
solution to the problem, since eq.(18.2) and eq.(20.2)
can be used to show that:
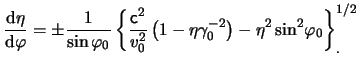 |
(21.1) |
In other words, the solution is the same as that already found
in eq.(17.14) and eq.(17.15) but with:
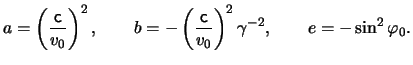 |
(21.2) |
Fig.(III.5) shows plots of the trajectory of the jet
for different values of its initial velocity.
Figure III.5:
Deflection of a relativistic
jet produced by its collision with an isothermal cloud
(semicircle). The jet is assumed to travel parallel to
the  axis at the moment it enters the cloud from
the right. In each plot different trajectories are shown
for different values of the initial height of the jet
axis at the moment it enters the cloud from
the right. In each plot different trajectories are shown
for different values of the initial height of the jet
 ,
, 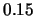 ,...,
,...,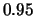 as measured from
the
as measured from
the 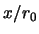 axis. The top, middle and bottom panel plots
were calculated for values of the initial velocity of the
jet
axis. The top, middle and bottom panel plots
were calculated for values of the initial velocity of the
jet
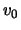 in units of the speed of light
in units of the speed of light
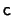 of
of 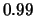 ,
, 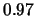 ,
, 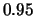 respectively.
respectively.
|
|
Let us now consider the case in which the gas in a galaxy is in hydrostatic
equilibrium with a dark matter halo. As it was shown in section
§19, for
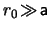 , the variation
of the pressure in the galaxy is given by eq.(19.5) and the
trajectory of the path of the jet is given by eq.(17.14) and
eq.(17.15) together with eq.(19.7) and the substitution
, the variation
of the pressure in the galaxy is given by eq.(19.5) and the
trajectory of the path of the jet is given by eq.(17.14) and
eq.(17.15) together with eq.(19.7) and the substitution
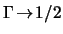 . Fig.(III.6) shows plots of
this for
. Fig.(III.6) shows plots of
this for
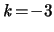 and different values of the initial
velocity of the jet
and different values of the initial
velocity of the jet
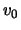 .
.
Figure III.6:
Trajectory of a relativistic jet as it crosses
a galaxy. The gas in the galaxy is assumed to be in
hydrostatic equilibrium with a gravitational potential given
by a dark matter halo in the galaxy. It is assumed that
the jet enters the galaxy parallel to the 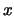 axis at a
height of
axis at a
height of
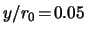 ,
, 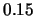 ,...,
,...,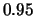 in different cases. The plots were calculated for the case
in which the parameter
in different cases. The plots were calculated for the case
in which the parameter
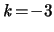 and the initial
velocity of the jet in units of the speed of light is
and the initial
velocity of the jet in units of the speed of light is 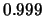 ,
, 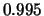 and
and 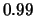 from top to bottom.
Continuous lines are analytic approximations to the problem
and dashed ones are direct numerical solutions.
from top to bottom.
Continuous lines are analytic approximations to the problem
and dashed ones are direct numerical solutions.
|
|
Sergio Mendoza Fri Apr 20, 2001
![\includegraphics[height=8.4cm]{fig.3.3.eps}](img601.png)
![]() , the variation
of the pressure in the galaxy is given by eq.(19.5) and the
trajectory of the path of the jet is given by eq.(17.14) and
eq.(17.15) together with eq.(19.7) and the substitution
, the variation
of the pressure in the galaxy is given by eq.(19.5) and the
trajectory of the path of the jet is given by eq.(17.14) and
eq.(17.15) together with eq.(19.7) and the substitution
![]() . Fig.(III.6) shows plots of
this for
. Fig.(III.6) shows plots of
this for
![]() and different values of the initial
velocity of the jet
and different values of the initial
velocity of the jet
![]() .
.
![\includegraphics[height=8.4cm]{fig.3.4.eps}](img606.png)